65001 - [NOIP2022] 喵了个喵meow
小 E 喜欢上了一款叫做《喵了个喵》的游戏。这个游戏有一个牌堆和 n 个可以从栈底删除元素的栈,任务是要通过游戏规则将所有的卡牌消去。开始时牌堆中有 m 张卡牌,从上到下的图案分别是 a_1, a_2,\dots, a_m。所有的卡牌一共有 k 种图案,从 1 到 k 编号。牌堆中每一种图案的卡牌都有偶数张。开始时所有的栈都是空的。这个游戏有两种操作:
- 选择一个栈,将牌堆顶上的卡牌放入栈的顶部。如果这么操作后,这个栈最上方的两张牌有相同的图案,则会自动将这两张牌消去。
- 选择两个不同的栈,如果这两个栈栈底的卡牌有相同的图案,则可以将这两张牌消去,原来在栈底上方的卡牌会成为新的栈底。如果不同,则什么也不会做。
这个游戏一共有 T 关,小 E 一直无法通关。请你帮小 E 设计一下游戏方案,即对于游戏的每一关,给出相应的操作序列使得小 E 可以把所有的卡牌消去。
输入
第一行包含一个正整数 T,表示数据组数。
接下来一共 T 组数据,在每组数据中:
第一行包含三个正整数 n, m, k,分别表示栈的个数、卡牌的个数、卡牌上图案的种类。
第二行包含 m 个正整数,分别表示 a_1, a_2,\dots, a_m,分别从上到下表示牌堆中卡牌的图案。
输入数据保证有解。
输出
对于每一组数据,输出若干行。
其中第一行包含一个正整数 \mathrm{op},表示操作的次数。你需要保证 m \leq \mathrm{op} \leq 2\times m。
接下来 \mathrm{op} 行,每行包含两个或三个正整数,整数之间用一个空格隔开。
若为两个整数 \texttt{1 s},则进行一次第一个操作并选择栈 s。
若为三个整数 \texttt{2 s1 s2},则进行一次第二个操作并选择栈 s_1 和 s_2。
你需要保证 1 \leq s, s_1, s_2 \leq n,且 s_1 \neq s_2。
样例
输入
1 2 4 2 1 2 1 2
输出
5 1 1 1 1 1 2 2 1 2 1 1
提示
【样例 1 解释】
下图是初始状态。

下图是前两次操作之后的结果。

下图是第三次和第四次操作之后的结果。
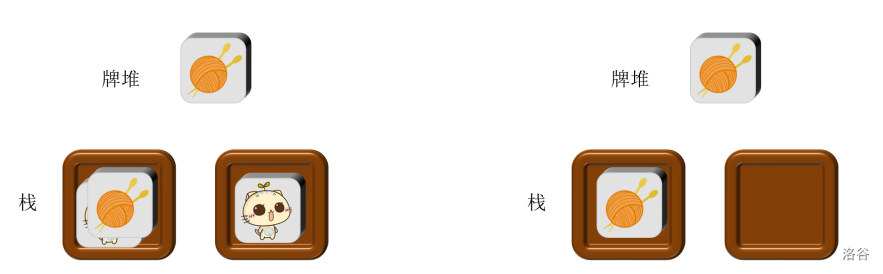
下图是第五次操作之后的结果。

【样例 2】
见选手目录下的 \texttt{meow/meow2.in} 与 \texttt{meow/meow2.ans}。
【数据范围】
设 S 为所有 T 组数据中 m 的总和。
对于所有数据,保证 S \leq 2 \times 10^6,1 \leq n \leq 300,1 \leq a_i \leq k。
| 测试点 | T= | n | k= | m \leq |
|---|---|---|---|---|
| 1\sim 3 | 1001 | \leq 300 | 2n-2 | 无限制 |
| 4\sim 6 | 1002 | =2 | 2n-1 | 无限制 |
| 7\sim 10 | 3 | =3 | 2n-1 | 14 |
| 11\sim 14 | 1004 | =3 | 2n-1 | 无限制 |
| 15\sim 20 | 1005 | \leq 300 | 2n-1 | 无限制 |
【评分方式】
对于每一组数据,若在按顺序进行所有操作后,牌堆为空且所有的栈均为空,则认为你的答案正确。
【提示】
你可以通过 T 的个位数来判断这个测试点是属于哪一类数据。
你的输出不需要与样例输出一致,输出任意一个合法解即可得分。
