2024年03月CCF-GESP编程能力等级认证C++编程八级真题
一、单选题(每题 2 分,共 30 分)
第 1 题 为丰富食堂菜谱,炒菜部进行头脑风暴。肉类有鸡肉、牛肉、羊肉、猪肉4种,切法有肉排、肉块、肉末3种,配菜有圆白菜、油菜、豆腐3种,辣度有麻辣、微辣、不辣3种。不考虑口感的情况下,选1种肉、1种切法、1种配菜、1种辣度产生一道菜(例如:麻辣牛肉片炒豆腐),这样能产生多少道菜?( )。
A. 13
B. 42
C. 63
D. 108
答案:D
第 2 题 已知袋中有2个相同的红球、3个相同的绿球、5个相同的黄球。每次取出一个不放回,全部取出。可能产生多少种序列?( )。
A. 6
B. 1440
C. 2520
D. 3628800
答案:C
第 3 题 以下二维数组的初始化,哪个是符合语法的?( )。
A. int a[][] = {{1, 2}, {3, 4}};
B. int a[][2] = {};
C. int a[2][2] = {{1, 2, 3}, {4, 5, 6}};
D. int a[2][] = {{1, 2, 3}, {4, 5, 6}};
答案:B
第 4 题 下面有关C++拷贝构造函数的说法,错误的是( )。
A. 必须实现拷贝构造函数,否则一定会出现编译错误。
B. 对象作为函数参数、以值传递方式传入函数时,会自动调用拷贝构造函数。
C. 对象作为函数返回值、以值传递方式从函数返回时,会自动调用拷贝构造函数。
D. 使用一个对象初始化另一个对象时,会自动调用拷贝构造函数。
答案:A
第 5 题 使用邻接表表达一个无向简单图,图中包含 v 个顶点、 e 条边,则该表中边节点的个数为( )。
A.v×(v-1)
B.v×v
C.2×e
D.e
答案:C
第 6 题 关于生成树的说法,错误的是( )。
A. 一个无向连通图可以有多个生成树。
B. 一个无向图,只要连通,就一定有生成树。
C.
在这里插入图片描述
D. n 个顶点的无向图,生成树包含 n-1 条边。
答案:D
第 7 题 已知三个 double 类型的变量 a 、 b 和 theta 分别表示一个三角形的两条边长及二者的夹角(弧度),则下列哪个表达式可以计算这个三角形的周长?( )。
A. a * b * sin(theta) / 2
B. a + b + (a + b) * sin(theta) / 2
C. a * b * cos(theta) / 2
D. a + b + sqrt(a * a + b * b - 2 * a * b * cos(theta))
答案:D
第 8 题 在有 n 个元素的二叉排序树中进行查找,其最好、最差时间复杂度分别为( )。
A. O(1)、O(n)
B. O(1)、O(log n)
C. O(log n)、O(log n)
D. O(log n)、O(n)
答案:A
第 9 题 如下图所示,半径为 r 、圆心角为 t (弧度)的扇形,下面哪个表达式能够求出顶部阴影部分的面积?()。
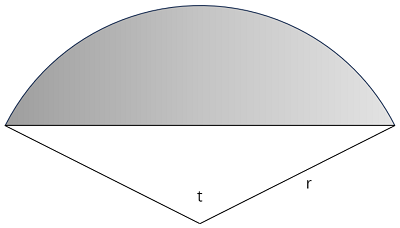
A. r * r * sin(t) / 2
B. r * r * t / 2
C. r * r * (t - sin(t))
D. r * r * (t - sin(t)) / 2
答案:D
第 10 题 下面程序的时间复杂度为( )。
int fib(int n) {
if (n <= 1)
return 1;
return fib(n - 1) + fib(n - 2);
}
A.O(2^n)
B.
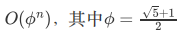
C.O(n)
D.O(1)
答案:B
第 11 题 下面程序的时间复杂度为( )。
int choose(int n, int m) {
if (m == 0 || m == n)
return 1;
return choose(n - 1, m - 1) + choose(n - 1, m);
}
A.O(2^n)
B.O(2^m×(n-m))
C.O(C(n,m))
D.O(m×(n-m))
答案:C
第 12 题 下面程序的时间复杂度为( )。
int primes[MAXP], num = 0;
bool isPrime[MAXN] = {
false
}
;
void sieve() {
for (int n = 2; n <= MAXN; n++) {
if (!isPrime[n])
primes[num++] = n;
for (int i = 0; i < num && n * primes[i] <= MAXN; i++) {
isPrime[n * primes[i]] = true;
if (n % primes[i] == 0)
break;
}
}
}
A.O(n)
B.O(n×logn)
C.O(n×loglogn)
D.O(n^2)
答案:A
第 13 题 下面程序的输出为( )。
#include <iostream>
using namespace std;
int a[10][10];
int main() {
int m = 5, n = 4;
for (int x = 0; x <= m; x++)
a[x][0] = 1;
for (int y = 1; y <= n; y++)
a[0][y] = 1;
for (int x = 1; x <= m; x++)
for (int y = 1; y <= n; y++)
a[x][y] = a[x - 1][y] + a[x][y - 1];
cout << a[m][n] << endl;
return 0;
}
A. 4
B. 5
C. 126
D. 3024
答案:C
第 14 题 下面程序的输出为( )。
#include <iostream>
using namespace std;
int main() {
int cnt = 0;
for (int x = 0; x <= 10; x++)
for (int y = 0; y <= 10; y++)
for (int z = 0; z <= 10; z++)
if (x + y + z == 15)
cnt++;
cout << cnt << endl;
return 0;
}
A. 90
B. 91
C. 96
D. 100
答案:B
第 15 题 下面的程序使用邻接矩阵表达的带权无向图,则从顶点0到顶点3的最短距离为( )。
int weight[4][4] = {
{ 0, 1, 7, 100},
{ 1, 0, 5, 15},
{ 7, 5, 0, 6},
{100, 15, 6, 0}};
A. 100
B. 16
C. 12
D. 13
答案:C
二、判断题(每题 2 分,共 20 分)
第 16 题 已知 int 类型的变量 a 和 b ,则执行语句 a, b = b, a; 后,变量 a 和 b 的值会互换。
答案:错误
第 17 题 一个袋子中有3个完全相同的红色小球、2个完全相同的蓝色小球。每次从中取出1个,再放回袋子,这样进行3次后,可能的颜色顺序有7种。
答案:错误
第 18 题 孙子定理是求解一次同余方程组的方法,最早见于中国南北朝时期(公元5世纪)的数学著作《孙子算经》。又称中国余数定理,是中国数学史上的一项伟大成就。
答案:正确
第 19 题 N个顶点的无向完全图有N×(N-1) 条边。
答案:错误
第 20 题 为解决哈希函数冲突,在哈希表项内设置链表存储该项内的所有冲突元素,则该哈希表内查找元素的最差时间复杂度为 O(1)。
答案:错误
第 21 题 求一个包含 v 个顶点、 e 条边的带权连通无向图的最小生成树,Prim算法的时间复杂度为 O(v × e)。
答案:错误
第 22 题
已知 int 类型的变量 a 、 b 和 c 中分别存储着一个三角形的三条边长,则这个三角形的面积可以通过表达式 sqrt((a + b + c) * (b + c - a) * (a + c - b) * (a + b - c)) / 4 求得。
答案:正确
第 23 题 可以使用深度优先搜索算法判断图的连通性。
答案:正确
第 24 题 在 N 个元素的二叉排序树中查找一个元素,平均情况的时间复杂度是 O(logN)。
答案:正确
第 25 题 给定 double 类型的变量 x ,且其值大于等于 1,我们可以通过二分法求出 logx 的近似值。
答案:正确
三、编程题(每题 25 分,共 50 分)
第 26 题 公倍数问题
第 27 题 接竹竿
