第十三届蓝桥杯大赛青少年4月省赛C++组试题真题(2022年)
一、选择题
第 1 题 单选题
下列关于类中声明的变量描述正确的是( )。
A. 只属于该类
B. 属于全局变量
C. 任何情况下都可被该类所有实例共享
D. 属于该类,某些情况下也可被该类不同实例所共享
第 2 题 单选题
下列对抽象类描述正确的是( )。
A. 抽象类没有构造方法
B. 抽象类必须提供抽象方法
C. 抽象类可以通过new关键字直接实例化
D. 有抽象方法的类一定是抽象类
第 3 题 单选题
二进制减法11101101-11001001( )。
A. 10111011
B. 11001001
C. 100100
D. 10101111
第 4 题 单选题
以下数据结构中,能够按照“先进后出”原则存取数据的是( )。
A. 栈
B. 队列
C. 二叉树
D. 循环队列
第 5 题 单选题
下列对int *p[3]描述正确的是( )。
A. p[3]表示数组的第3个元素的值,是int类型的值
B. p是一个具有3个元素的指针数组,每个元素是一个int 类型指针
C. p是一个指向数组的指针,所指向的数组是3个int 类型元素
D. p是一个指向某数组中第3个元素的指针,该元素是int 型变量
二、编程题
第 6 题 问答题
统计数字
题目描述:
给定一个正整数N,找出3到N之间的正整数中,个位数为3的有多少个。
例如:N=25,3至25之间个位数为3的有3、13、23,一共有3个。
输入描述:
输入一个正整数N(3≤N≤99993)输出描述:
输出一个整数,表示3到N之间的正整数中,个位数为3的个数(包括3和N)
样例输入:
25
样例输出:
3
第 7 题 问答题
字母组合
题目描述:
给定N个小写字母,然后将N个小写字母按照字典排序后组合成一个字符串并输出。
例如N=4,4个小写字母分别为c,d,a,c,按照字典排序后组合成的字符串为:accd
输入描述:
第一行输入一个正整数N(2 < N < 100),表示小写字母的个数
第二行输出N个小写字母,且小写字母之间以一个空格隔开
输出描述:
将N个小写字母按照字典排序后组合成一个字符串并输出
样例输入:
4
c d a c
样例输出:
accd
第 8 题 问答题
组合
题目描述:
某商家将一种汤圆按照数量不同,分装成N种规格来售卖。这样的售卖方式会限制一些数量的汤圆不能买到。
例如:
N=2,2种规格的汤圆分别装3个和5个,这种情况下限制了1,2,4,7四种数量的汤圆不能买到。
给出N及N种规格的汤圆数量,请计算出有多少种数量的汤圆不能买到,如果有无限种数量的汤圆不能买到就输出“-1”。
输入描述:
第一行输入一个正整数N(1 < N < 20),表示有N种规格的汤圆
第二行输入N个各不相同的正整数(1 < 正整数 < 100),表示每种规格的汤圆数量,且正整数之间以一个空格隔开
输出描述:
输出在这种情况下有多少种汤圆数量是不能买到的,如果有无限种数量的汤圆不能买到就输出“-1”
样例输入:
2
3 5
样例输出:
4
第 9 题 问答题
帮助
题目描述:
已知有M名需要帮助的贫困学生,及每名学生购买图书的金额;和N位愿意提供帮助的志愿者,及每名志愿者愿意帮助的金额。
现N名志愿者认领贫困生进行帮助,每人可以认领贫困学生的名额不限,但如果志愿者愿意帮助的金额小于每名贫困生购买图书的金额,那么该志愿者不能认领贫困学生。请你计算出这些志愿者最多可以认领多少名贫困学生(一名学生只能被一名志愿者认领)。
例如:M=5,N=2
5名贫困学生购买图书金额分别是:200、145、240、50、45,2名志愿者帮助金额分别为150、300。则最多可以认领4名学生。(金额300的志愿者认领200、50、45这3名学生,金额150的志愿者认领145这1名学生)
输入描述:
第一行输入一个正整数M(1 < M < 200),表示有M名贫困学生
第二行输入M个正整数(10 < 正整数 < 300),表示每名贫困生需要购买的图书金额,正整数之间一个空格隔开
第三行输入一个正整数N(1 < N < 50),表示有N名志愿者
第四行输入N个正整数(10 < 正整数 < 10000),表示N名志愿者帮助的金额,正整数之间一个空格隔开
输出描述:
输出一个整数,表示N名志愿者最多可以认领多少名贫困学生
样例输入:
5
200 145 240 50 45
2
150 300
样例输出:
4
第 10 题 问答题
路线
题目描述:
有一个旅游景区,景区中有N个景点,景点以数字1到N编号,其中编号为N的景点为游客服务中心所在地。景区中有M条连接路线,每条路线连接两个景点。
已知:
1)一个景点可以被多条路线连接;
2)景点之间的连接路线都可以双向行走;
当给出N个景点和M条连接路线,及M条路线的连接关系,请你计算出从编号1到编号N-1的每一个景点,到达游客服务中心至少需要经过几条路线,如果某个景点不能到达游客服务中心则输出“-1”。
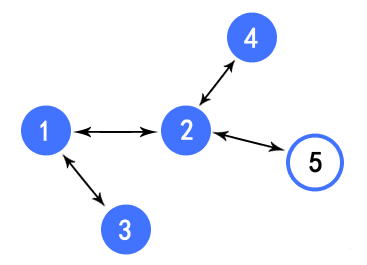
例如:N=5,M=4,4条路线的连接关系为:1<->2、1<->3、2<->4、2<->5,
景点1到达景点5(游客服务中心)至少经过2条路线(路线2、路线4);
景点2到达景点5(游客服务中心)至少经过1条路线(路线4);
景点3到达景点5(游客服务中心)至少经过3条路线(路线1、路线2、路线4);
景点4到达景点5(游客服务中心)至少经过2条路线(路线3、路线4);
输入描述:
第一行输入两个正整数N和M(4<=N<=100,1<=M<=100),N表示景点个数,M表示路线条数,两个正整数之间一个空格隔开
接下来输入M行,每行包括两个正整数S,E(1≤S≤N,1≤E≤N,S!=E),两个正整数之间一个空格隔开,表示编号S和编号E的两个景点有一条路线连接
输出描述:
一行输出多个整数。按照1到N-1的编号顺序,分别输出每个景点到达编号N(游客服务中心),经过几条路线可以到达,如果某个景点不能到达则输出“-1”,整数之间一个空格隔开
样例输入:
5 4
1 2
1 3
2 4
2 5
样例输出:
2 1 3 2
第 11 题 问答题
奖品
题目描述:
有一个N*M的矩阵方格,其中有些方格中有奖品,有些方格中没有奖品。小蓝需要从N*的矩阵中选择一个正方形区域,如果所选的正方形区域的一个对角线方格中都有奖品,其他方格都没有奖品,就会获得所选区域中的所有奖品,否则不能获得奖品。
当给出N和M的值,及N*M的矩阵方格中摆放的奖品情况(0表示方格中没有奖品,1表示方格中有奖品),请你帮助小蓝找出一个正方形区域,能够获得数量最多的奖品,并将奖品数输出。
例如:N=5,M=6,奖品情况如下:
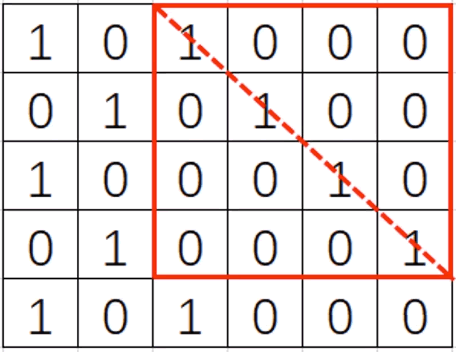
选择上图红色正方形区域,可以获得最多的4个奖品。
输入描述:
第一行输入两个整数N和M(1≤N≤100,1≤M≤100),N表示矩阵的行数,M表示矩阵的列数,两个整数之间一个空格隔开,接下来输入M行,每行包括M个0或者1(0表示方格中没有奖品,1表示方格中有奖品),0或者1之间一个空格隔开
输出描述:
输出一个整数,表示最多可以获得的奖品数
样例输入:
5 6
1 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
0 1 0 0 0 1
1 0 1 0 0 0
样例输出:
4
