第十三届蓝桥杯大赛青少年第一场省赛C++组试题真题（2022年）

2023年06月02日

一、选择题

第 1 题单选题

以下对main函描述正确的是（）。

A. main 函数必须写在所有函数的前面

B. main 函数必须写在所有函数的后面

C. main函数可以写在任何位置，但不能放到其他函数里

D. main函数必须卸载固定位置

第 2 题单选题

已知char a；float b；double c;执行语句c=a+b+c；后变量c的类型是（）。

A. char

B. float

C. double

D. int

第 3 题单选题

二进制数1101111转换为十六进制是（）。

A. 157

B. 111

C. 6f

D. 3fe

第 4 题单选题

下列函数中哪一个不能重载（）。

A. 构造函数

B. 析构函数

C. 成员函数

D. 非成员函数

第 5 题单选题

下列指针的用法中哪一个不正确（）。

int i；int *p=&i；

int i；int *p；i=*p;

int *p；p=0；

int i=5；int *p; p=&i;

二、编程题

第 6 题问答题

比较大小

题目描述：

给定两个正整数N和M（0 < N < 200，0 < M < 200，N!=M），比较两个正整数的大小，然后将较大的一个正整数输出。

例如：N=145，M=100，比较后145大于100，故输出145。

输入描述

输入两个正整数N和M（0 < N < 200，0 < M < 200，N!=M），正整数之间一个空格隔开。

输出描述

输出一个正整数，表示N和M中较大的一个正整数

样例输入：

145 100

样例输出

第 7 题问答题

分解整数

题目描述：

给定一个正整数N，然后将N分解成3个正整数之和。计算出共有多少种符合要求的分解方法。

要求：

1）分解的3个正整数各不相同；

2）分解的3个正整数中都不含数字3和7。

如：N为8，可分解为（1，1，6）、（1，2，5）、（1，3，4）、（2，2，4）、（2，3，3），其中满足要求的分解方法有1种，为（1，2，5）。

输入描述！

输入一个正整数N（5 < N < 501），表示需要分解的正整数

输出描述

输出一个整数，表示共有多少种符合要求的分解方法

样例输入

样例输出

第 8 题问答题

组合

提示信息：

因数：因数是指整数a除以整数b（b!=0）的商正好是整数而没有余数，我们就说b是a的因数。

公因数：给定若干个整数，如果有一个（些）数是它们共同的因数，那么这个（些）数就叫做它们的公因数。

互质数：公因数只有1的两个非零自然数，叫做互质数；例如：2和3，公因数只有1，为互质数。

题目描述：

某商店将一种糖果按照数量打包成N和M两种规格来售卖（N和M为互质数，且N和M有无数包）。这样的售卖方式会限制一些数量的糖果不能买到。那么在给出N和M的值，请你计算出最多不能买到的糖果数量。

例如：

当N=3，M=5，3和5为互质数，不能买到的糖果数量有1，2，4，7，最多不能买到的糖果数量就是7，7之后的任何数量的糖果都是可以通过组合购买到的。！

输入描述！

输入两个正整数N，M（2 < N < M < 100，N和M为互质数），表示两种规格的糖果数量，正整数之间一个空格隔开

输出描述

输出一个整数，表示最多不能买到的糖果数量！

样例输入

3 5

样例输出

第 9 题问答题

最大值

题目描述：

手工课上老师拿出N张长方形彩纸，且每张彩纸上都画着W*H的网格（网格铺满整张彩纸）。现在老师将N张彩纸裁剪出K张大小相同的正方形，并且要使裁剪出的正方形的边长最大（裁剪的正方形边长必须为整数）。

例如：N=2，有2张彩纸，第一张彩纸W=4，H=3；第二张彩纸W=5，H=4；K=6，裁剪的6个正方形边长最大是2。

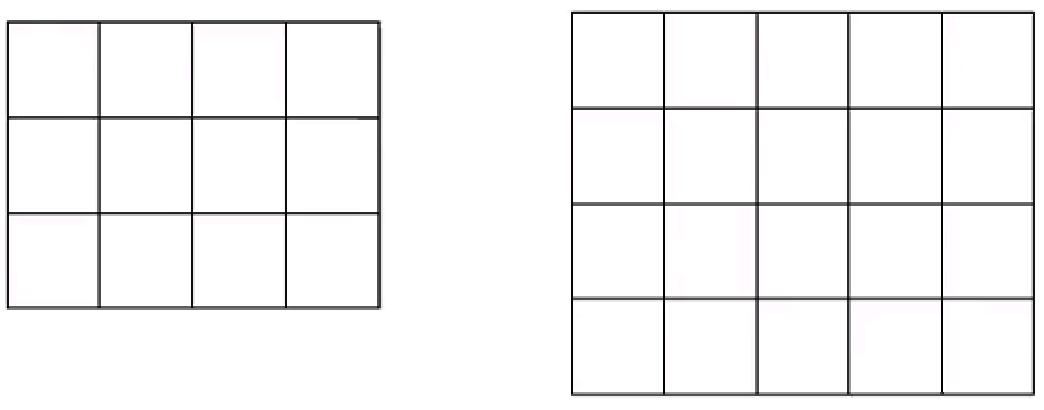
当给出N张长方形彩纸W和H，及K的值，请计算出将N张彩纸裁剪出K张大小相同的正方形，正方形的边长最大是多少（裁剪的正方形边长必须为整数）。

输入描述

第一行输入两个正整数N，K（1 < N < 100，1 < K < 100），N表示彩纸数量，K表示需裁剪的正方形数量，两个正整数之间一个空格隔开

第二行开始，输入N行，每行输入两个正整数Wi，Hi（1 < Wi < 1000，1 < Hi < 1000，且Wi!=Hi），Wi表示彩纸的长度，Hi表示彩纸的宽度，两个正整数之间一个空格隔开

输出描述

输出一个正整数，表示将N张彩纸裁剪出K张大小相同的正方形的边长最大是多少（裁剪的正方形边长必须为整数），如果不能裁剪出K张正方形就输出“-1"。

样例输入

2 6
4 3
5 4

样例输出

第 10 题问答题

农作物

题目描述：

有一块农田被划分为N*M块，农作物和杂草分布生长在农田中，其中农作物使用大写字母“R”表示，杂草使用大写字母“X“表示。请计算出农田中有几块独立的农作物区域（独立的农作物区域指该区域上下左右都被杂草围住，且N*M以外的区域都是杂草）。

例如：N=4，M=4，4*4的农田中农作物和杂草分布如下图：

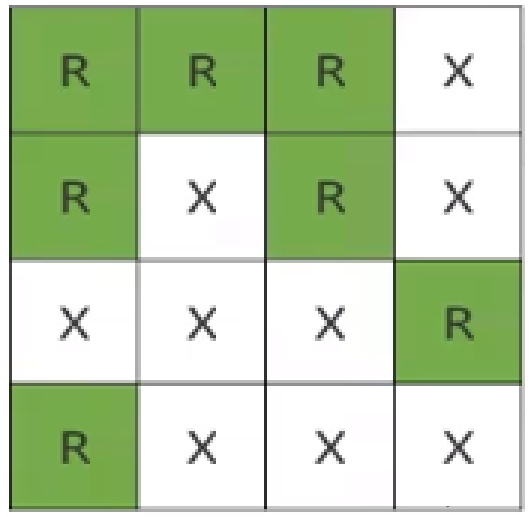
这块4*4的农田中有3块独立的农作物区域（绿色的3部分）。

输入描述

第一行输入两个整数N和M（15Ns100，15M≤100），N表示农田的行数，M表示农田的列数，且两个正整数之间一个空格隔开。

接下来的N行每行包括M个字符（字符只能为R或X），R表示农作物，X表示杂草，字符之间一个空格隔开。

输出描述

输出一个整数，表示N*M的农田中有几块独立的农作物区域

样例输入

4 4
R R R X
R X R X
X X X R
R X X X

样例输出

第 11 题问答题

编程实现：面积

题目描述：

小蓝要给墙面上的N个矩形区域粉刷涂料，给出每个矩形左下角和右上角的两个坐标（x1，y1，x2，y2）。请帮助小蓝计算下粉刷涂料的面积是多少，如果矩形之间有重叠部分只计算一次。

例如：有2个矩形，2个矩形左下角和右上角的两个坐标分别为：（2，2，9，5）、（6，1，12，9），其粉刷涂料的面积是60。

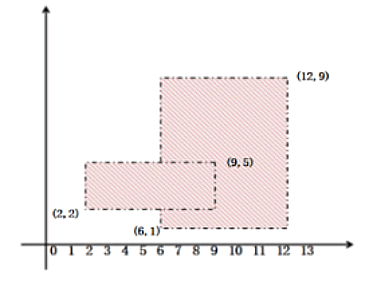
输入描述

第一行输入一个整数N（2<=N<=20），表示有N个矩形

接下来的N行每行包括四个正整数x1，y1，×2，y2（0<=x1，y1，x2，y2<=100，且x1!=x2，y1!=y2），x1和y1表示矩形左下角的坐标，x2和y2表示矩形右上角的坐标，四个正整数之间一个空格隔开

输出描述

输出一个整数，表示N个矩形需要粉刷的面积，重叠部分只计算一次！

样例输入

2
2 2 9 5
6 1 12 9

样例输出