65015 - [CSP-S 2021] 交通规划 traffic
给定一个平面上 n 条水平直线和 m 条垂直直线,它们相交形成 n 行 m 列的网格,从上到下第 r 条水平直线和从左到右第 c 条垂直直线之间的交点称为格点 (r, c)。网格中任意两个水平或垂直相邻的格点之间的线段称为一条边,每条边有一个非负整数边权。
进行 T 次询问,每次询问形式如下:
给出 k(T 次询问的 k 可能不同)个附加点,每个附加点位于一条从网格边缘向外出发的射线上。所有从网格边缘向外出发的射线按左上-右上-右下-左下-左上的顺序依次编号为 1 到 2 n + 2 m,如下图:
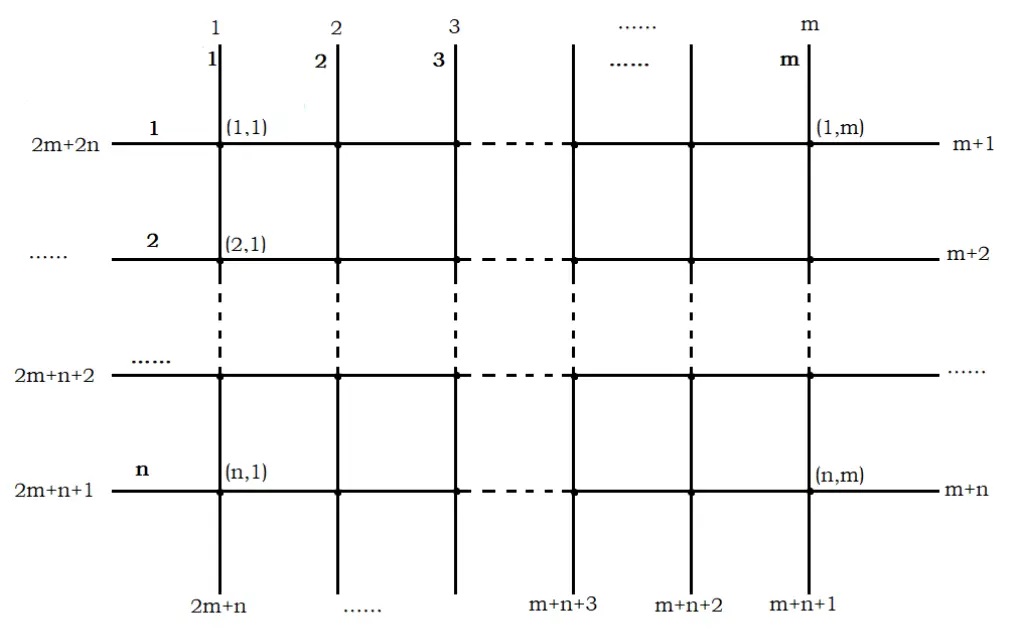
对于每次询问,不同附加点所在的射线互不相同。每个附加点和最近的格点之间的线段也称为一条边,也有非负整数边权(注意,在角上的格点有可能和两个附加点同时相连)。
给定每个附加点的颜色(黑色或者白色),请你将网格内每个格点的颜色染成黑白二者之一,并使得所有两端颜色不同的边的边权和最小。请输出这个最小的边权和。
Input
第一行,三个正整数 n, m, T,分别表示水平、垂直直线的数量,以及询问次数。
接下来 n - 1 行,每行 m 个非负整数。其中第 i 行的第 j 个非负整数 {x 1}_{i, j} 表示 (i, j) 和 (i + 1, j) 间的边权。
接下来 n 行,每行 m - 1 个非负整数。其中第 i 行的第 j 个非负整数 {x 2}_{i, j} 表示 (i, j) 和 (i, j + 1) 间的边权。
接下来依次输入 T 组询问。第 i 组询问开头为一行一个正整数 k_i 表示这次询问附加点的总数。接下来 k_i 行每行三个非负整数。其中第 j 行依次为 {x 3}_{i, j}, p_{i, j}, t_{i, j} 表示第 j 个附加点和相邻格点之间的边权、所在的射线编号以及附加点颜色(0 为白色,1 为黑色)。保证同一组询问内 p_{i, j} 互不相同。
每行的多个整数由空格分隔。
Output
输出 T 行,第 i 行输出一个非负整数,表示第 i 次询问染色之后两端颜色不同的边权和的最小值。
Examples
Input
2 3 1 9 4 7 3 8 10 5 2 19 3 1 17 9 0
Output
12
Hint
【样例解释 #1】
最优方案:(1, 3), (1, 2), (2, 3) 为黑色;(1, 1), (2, 1), (2, 2) 为白色。
【数据范围】
| 测试点编号 | n, m \le | k_i \le |
|---|---|---|
| 1 \sim 2 | 5 | 50 |
| 3 \sim 5 | 18 | 2 |
| 6 \sim 8 | 18 | 50 |
| 9 \sim 10 | 100 | 2 |
| 11 \sim 12 | 100 | 50 |
| 13 \sim 16 | 500 | 2 |
| 17 \sim 20 | 500 | 50 |
对于所有数据,2 \le n, m \le 500,1 \le T \le 50,1 \le k_i \le \min { 2 (n + m), 50 },1 \le \sum_{i = 1}^{T} k_i \le 50,0 \le x \le {10}^6,1 \le p \le 2 (n + m),t \in { 0, 1 }。
保证对于每个 i \in [1, T],p_{i, j} 互不相同。
